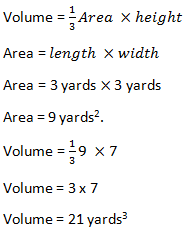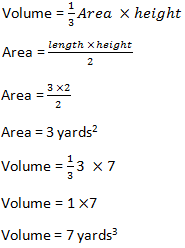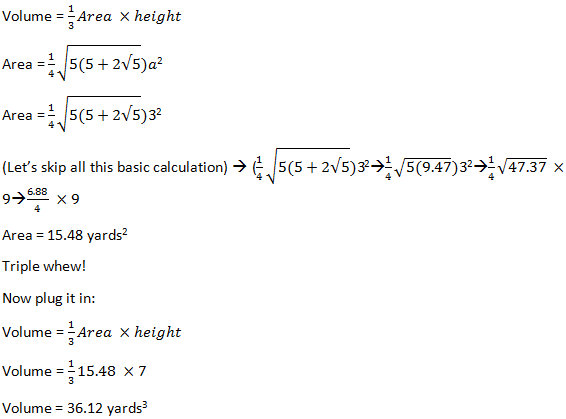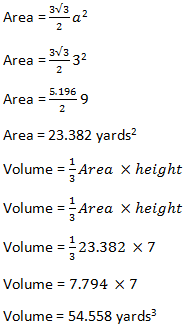We all heard it before:
Hi diddle diddle,
The pyramid’s riddle:
If a cow jumped over the moon
Times that by three
Or more, to see,
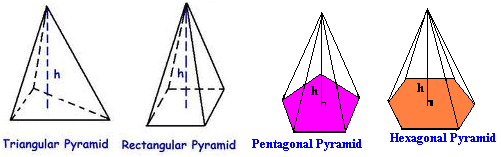
The volume of moonlight to spoon?
The volume of a pyramid is easier than you think! It doesn’t matter if the pyramid has a square base, rectangular base, a triangular base, or any other base, the general formula is the same.
The only catch is that the bases might have different shapes. To keep it simple, we’ll stay with the “classic” formulas.
- So, what is the area of a square or a rectangle?
Area = length x width
- What is the area of a triangle?
(For many more calculations for the area of a triangle, check out my blog here!)
- What is the area of a pentagon?
For simplicity’s sake, let’s say have one only the length of one of the five sides,
- What is the area of a hexagon?
For simplicity’s sake, let’s say have one only the length of one of the six sides,
Whew! Am I glad that’s over with.
Let’s plug in one number and see what we get. Let’s say that the side of each of these pyramids has a value of 3 yards. For the triangle, we need a “height” for the base, and we’ll give that a value of 2 yards. For the pyramidal height, let’s say they’re really tall—maybe 7 yards.
Let’s plow right through these:
Volume of a Pyramid: Square pyramid
Don’t forget the small “3” for the yards—we are dealing in three dimensions here!
Volume of a Pyramid: Triangular pyramid
Volume of a Pyramid: Pentagonal Pyramid
OKAY! LAST ONE!!!! By the way, if this is confusing, we recommend getting some equations homework help.
Volume of a Pyramid: Hexagonal pyramid
Yikes! Without an online math tutor, that’s a lot of moonlight to cover. Better start scooping!