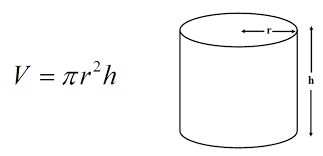One of the simple joys of life is a push-pop candy. You remember ‘em:
Right, a lollipop without a stick.
And while it sounds like a push-up, a Push-Pop doesn’t have the same effect.
(And no, eating one does not have the same effect as doing an actual push-up).
Back when I was a kid, I always wondered how much good stuff was in a tube. Thanks to the wonders of a simple math formula to calculate the volume of a cylinder, we can solve this burning question! It isn’t quite the same as calculating the volume of a cone, but it’s still feasible.
CAVEAT: (Ideally, the candy went all the way to the bottom of the tube, but we kids knew this was never the case. ☹)
Here’s the formula for the volume of a cylinder:
Hmmmm, this may look familiar to some of you. Here’s why:
This is a cylinder. It’s basically a tube that has the same width at every point. When you look at the end points, they are perfect circles.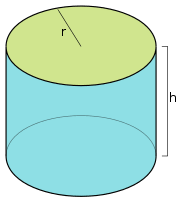
We know the formula for finding the area inside of a circle, right? If that doesn’t ring a bell, it might be a good idea to get some equations homework help. r is simply the radius, or a straight line from the edge of the circle to the center.
Once we find out the area of a circle, we just extend it into a third dimension, which is the height. Multiplying the area by the height gives us the volume!
Let’s go back to our push-up candy!
Let’s assume I haven’t eaten it already.
Mine looks to be about 1.75 cm across and 4.5 cm tall. Yeah, they’re not as big as they used to be.
Here’s the formula: V = Πr2h
Make sense? If not, this would be a good time to message an online math tutor. Since we know the diameter is 1.75 centimeters per pop, we can simply cut the number in half to get the radius.
1.75 ÷ 2 = 0.875 centimeters
Now, plug in the numbers:
V = Πr2h
V = Π0.8752 x 4.5
V = Π0.765625 x 4.5
V = Π x 3.4453125
V = 3.14 x 3.4453125
V = 10.82 cm3
Don’t forget the little 3 after the label. We are calculating in three dimensions.
Hurrah for the volume master! Time for a treat!