Math Help: How to Find the Surface Area of a Triangular Prism

Baa baa, black sheep,

Have you any wool?

“Yes sir, but sir,

The storage tent is full.

Build me another,

All the way ‘round,

So no wool is on the ground.”

Yeesh! What a bossy sheep! But he has a point. We don’t want any of that wool exposed to bugs and rainwater.

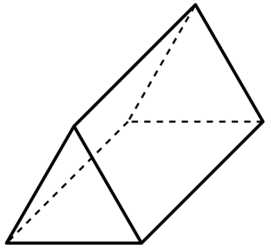
Here’s what the sheep has in mind. It’s a triangular prism:

So, that leaves us needing to figure out how much canvassing we need to make the cover. In other words, what is the surface area of the tent?

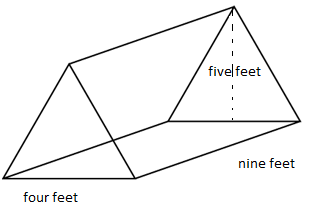
The sheep has the dimensions for the previous tent: 4 feet wide, 5 feet high, and 9 feet long. Like so:

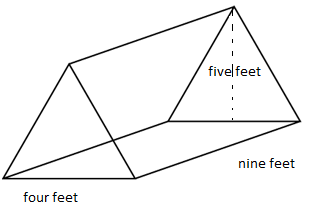
To calculate the surface area of a triangular prism, we need to add the areas of all the shapes that make up this prism.

First of all, we need to cover the ground. We can see that this is a rectangle...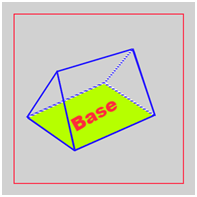

The area of a rectangle is the length x width

We have two end flaps. They are triangles.

The area for a triangle is,
:

The sides are slanted, but they are still rectangle We know this because the top of the tent is the same length as the bottom of the tent.

So, their area is length x width

This might seem like a lot of steps, but it is actually easy! Let’s start with the bottom rectangle
length x width

4 x 9 = 36 feet²

*Don’t forget the little 2 since we are dealing with two dimensions!

Now the triangles that form the front and back flaps!

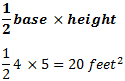
**We have two flaps, so we need to multiply this number by 2. To better understand why, we recommend getting some equations homework help.

The two slides are slightly complicated. We know that the rectangles are 9 feet long, but we don’t have the lengths of the slants.

But we can figure it out easily! Let’s look at the prism again.

The slanted side is the hypotenuse of the front and back triangle flaps. We can easily find the hypotenuse with the Pythagorean Theorem!

The theorem is for right triangles. The front flap is not a right triangle, so let’s cut it in half to get a 90^o!

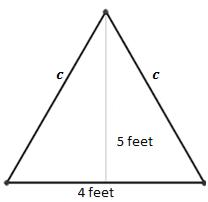
Each half is now TWO feet long but the height is still the same: FIVE feet.

Are you with me? Message an equations tutor to get this 100% clear. Otherwise, let’s plug these into the Pythagorean Theorem to get the answer!

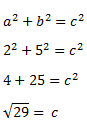
All right!

Now let’s put this figure into our equation for the area of a rectangle!
length x width

And if you need to figure out how much cubic feet of wool our new tent can hold, check out the blog on how to figure out the volume of a triangular prism here!