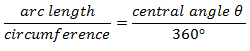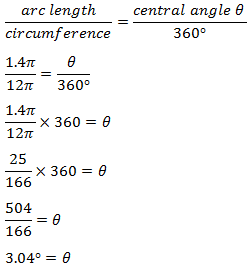Three Little Kittens
Found their Mittens
So they shall have some pie.
Said one, “The size for me
is an arc from A to B
and just shy of 360!”
Not quite sure what this little kitten was going on about?
Well, the central angle is one way we can use to measure circles.
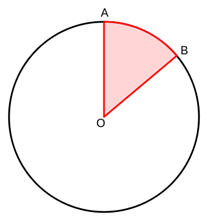
As the name suggests, it is an angle with the vertex at circle’s center. Like this:
Here, we can see that the vertex is the center of the circle, with points A and B on the outer edge. Each side of angle ∠AOB is a radius, which means that it is half of the diameter.
The outer edge of the circle between points A and B—the kitten’s pie crust—is an arc. The arc length is the measurement between A and B along the curve.
Okay, now that we know the terms cold, let’s set up some relationships.
We can make up some ratios. The arc length from AB is a portion of the entire circumference. There is a direct ratio between the circumference of a circle and its measurement of degrees. The A circle has 360°. The central arc is a portion of that.
Let’s say we know the arc length was 25π and the circumference was 166π. We can calculate the central angle easily, but if you’re stuck our tutors can assist with math homework help.
What if we only knew the length of one side of an angle and the arc length?
This is a bit more challenging, but it’s just an extra step.
Let’s recap with our original angle & circle:
Say OA was 6 feet. Arc length is 1.4π
We can calculate the circumference of the circle: Circumference = Diameter x π
The radius is half the diameter, and we know that AO is a radius because it extends from the center of the circle at point O and reaches the outer edge at point A.
Circumference = Diameter x π = 2(radius) x π
Circumference = 2(6 feet) x π
Circumference = 12π
Great job! Now, we can plug in the numbers into our original geometry formula!
Yep, pretty small angle, all right. Let’s hope that’s not the one our kitty ended up with!