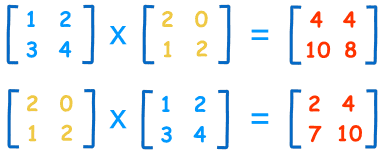If you’ve survived the perils of trigonometry and plunged into the depths of pre-calculus, you’ve probably encountered a matrix, or two matrices, at some point in your math career. You already understand why college algebra matters, but what about the other subjects? Once you’ve mastered the relatively simple task of adding multiple numbers within matrices, your next step is to start matrix multiplication, which gets a bit trickier. Not to worry! If you follow this step-by-step process to solve matrix multiplication, you’ll become a master of matrices big and small before you know it.
Matrix Multiplication Step 1: Decide if you can, in fact, multiply the matrices in front of you.
Matrices can only be multiplied if the first matrix has the same number of columns as the number of rows in the second matrix. When you first begin matrix multiplication, you’ll usually be faced with two identical matrices, but keep this rule in mind when you start multiplying matrices of different sizes.
Matrix Multiplication Step 2: Decide how large your end solution will be.
Again, when you first start matrix multiplication, your solution matrix will be identical to the two you multiplied. However, when faced with different sized matrices, your solution matrix will have the same number of rows as the first matrix, and the same number of columns as the second matrix.
We should stop and mention that at this point if the content isn’t making sense, it would be a good idea to get some precalculus homework help.
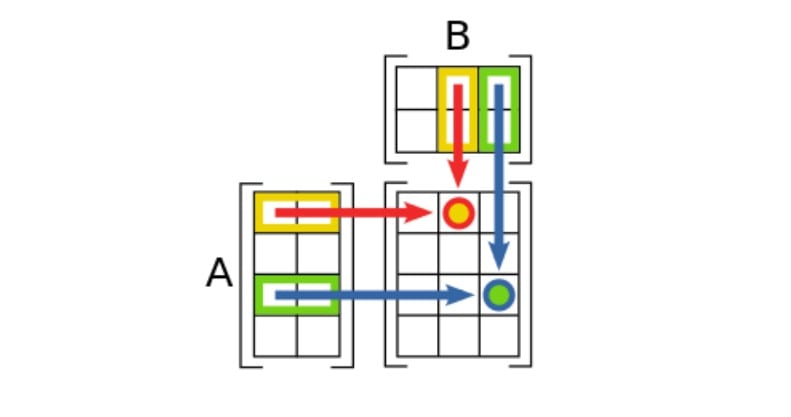
Matrix Multiplication Step 3: Find the dot products.
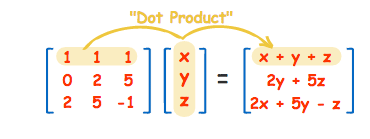Outline the first row in the first matrix, and the first column in the second matrix. To get the first value in your solution matrix, first multiply the first number in the first matrix by the first number in the second matrix. Afterwards, multiply the second number in the first matrix by the second number in the second matrix. Add those two values together, and you’ve got your first dot product. Use this method to work through the remaining rows and columns of your matrices.
Matrix Multiplication Step 4: Remember to simplify.
You’re almost done! If you work best by writing your work down in small steps, remember that your final matrix should only include your final dot products. Feel free to physically write down your multiplication thought process, but in a separate matrix.