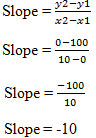Jack and Jill
went up a hill
To fetch a pail a water.
But Jack looked down
At the sloping ground
And said, “Slope’s -10, let’s go sledding after.”
Jack wasn’t just wishing on the fly. He knew a good slope of a line when he saw it.
But what is slope? Why is it important? And how do we calculate the slope of a line?
The definition of slope is pretty easy. It’s just a surface in which one point is at a higher elevation than another. When you go up or down the side of a hill—ala Jack and Jill—you’re traveling on a slope. All of these are slopes:
Okay, so why is it so important?
Well, calculating slope is helpful in the real world. If you’re designing a race car to accelerate uphill, you can figure out how much horsepower you’ll need.
If you’re charting progress based against time, you can monitor the rate.
The larger the slope, the greater the change, the smaller the slope, the lesser the change.
So, what’s the formula?
On a chart, slope is the change in y axis divided by the change in the x axis.
Or like this:
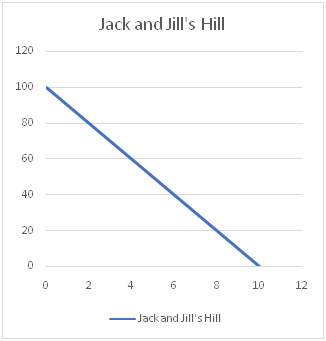
It might not seem like it now, but using algebra to find the slope of a line will matter in your career some day. You can get equations homework help if this doesn’t make sense. For now, let’s see what Jack meant. Here’s his hill:
Slope is defined as Rise (y-axis) over Run (x-axis). We’re going downhill, starting on the top and ending on the bottom. We’ll say the hill is 100 feet high. So the graph would look like this:
This means that at zero seconds, Jack and Jill were at the top of the hill. He calculated it would take them 10 seconds to reach the bottom of the hill, which is ground level 0.
Let’s plug in the numbers:
Bonus question: should Jack and Jill go down the hill?
We know the slope of their hill is -10. But what exactly does that mean? One way we can look at it is in terms of safety. Is a slope with 10 safe?
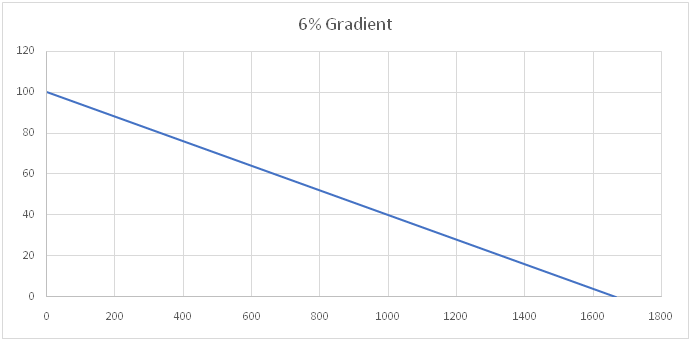
Let’s convert the slope to a gradient. Gradient is what is used to measure roadways. For a comparison, in the U.S., the maximum gradient for a slope is generally 6%.
How do we calculate gradient? Easy: just multiply the slope by 100 to get a percentile.
A 6% gradient looks like this:
Fun fact: the steepest road in the U.S. has a 37% gradient, with 9 runner-ups in the 30 percentile.
Let’s find out the gradient for Jack’s and Jill’s Hill. We’ll use a positive value to remain consistent.
Gradient = slope X 100
Gradient = 10 x 100
Gradient = 1000% !!!
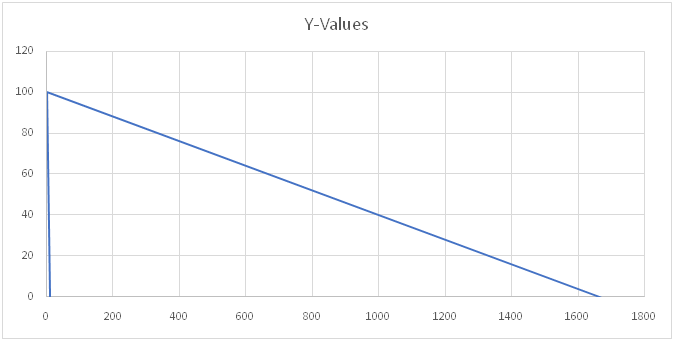
Let’s overlay Jack’s calculation on the official U.S. maximum and see what we get:
One thing’s for sure: they’re in a for a heck of a ride down! Will cooler heads prevail?
Let’s see how it ends:
Jill looked down
And with a frown,
Called Jack a crazy fool.
“Your plan’s unsound,
You’ll break your crown!”
And told him to go back to school.