Online Learning: Mastering Angle Types with Examples

There’s something to be said about angles:

“To think I will never see

An angle as complementary as thee.

An angle whose hungry mouth is open

To a supplementary pair unbroken

With a line, perpendicular or straight,

We a newborn angle doth create!”

While poets may sing the praise of angles, let’s set it down in basic terms.

• What’s an angle?

An angle is the measurement of degrees between two lines.

These are all angles. They are acute angles because the gaps between the two lines are less than 90^o. Acute means small, and small things are cute. Aren’t they cute?

These are angles, too. They are obtuse angles because the gaps between the two lines are GREATER than 90^o. Obtuse means “slow” and “unintelligent.” While we don’t want to be mean to our angles, we can think of them as a bit unwieldly and hard to manage. Why are these angles so obtuse, darn it?!?

This means that angles that are EXACTLY 90^o are called right angles. As Goldilocks would tell us, not too large, not too small, just right. We can make little squares inside them to show that the corner is 90^o sharp. Pretty cool, huh?

OKAY, now that we have that downpat, what do we do with our happy angle family?

• We can use angles to measure degrees.

For designers like architects, builders, and engineers, this is essential stuff…and for obvious reasons. If you’re measuring space and distance, whether for landscaping or for algorithms, angles are a must.

Let’s throw some basic math calculations on how to measure angles.

• Adjacent Angles

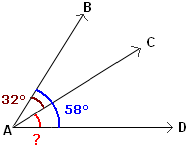
These are pretty simple. It’s literally two angles next to each other! They share a common vertex (the point where they intercept) and one side. Here’s one:

For example, we see that the blue angle,∠BAD, has a measurement of 58^o. The smaller angle ∠BAC has a measurement of 32^o.  What is the measurement of ∠CAD?

Simply subtract!

58^o – 32^o = 26^o

Easy, right?

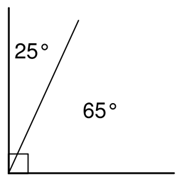
• Complementary Angles

A complementary angle is a specific type of adjacent angle. These angles add up to 90^o to form a RIGHT ANGLE.  Here’s one:

Since we know that the sum of the angles is always 90^o, we can easily find out what one angle measurement is if we know the other. Since both angles are smaller than 90^o, we know that all angles in complementary angles are acute.

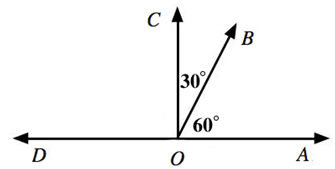
• Supplementary Angles

Supplementary Angles take things a bit further. When we put two COMPLEMENTARY ANGLES together, they form a straight line, like this:

See how CO bisects DA? The angles on the right of ∠COA add up to 90^o, right? That means that ∠DOC is also 90^o. Put them together and we have supplementary angles.  Angles that are supplementary share the same vertex and one line. They form a straight line and add up to 180^o. Dead on arrival, no?

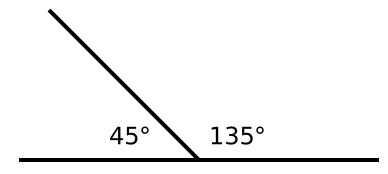
Here’s another example of a supplementary angle, this time, without complementary angles.

Note that if one angle is less than 90^o, the other must be greater than 90^o to add up to 180^o. Thus, unless the angles are right angles, supplementary angles include one ACUTE and one OBTUSE angle.

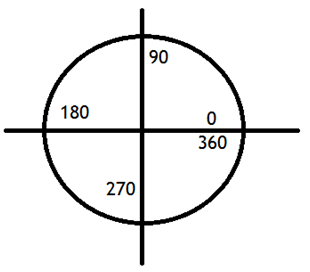
We can also complicate this by stating that in a circle, all the angles add up to 360. This is because two right angles sharing a vertex forms a straight line, but travels half a circle. If we join two more right angles at the same vertex, the degrees of measurement would go all the way around! Like this:

Got it? Right on target!

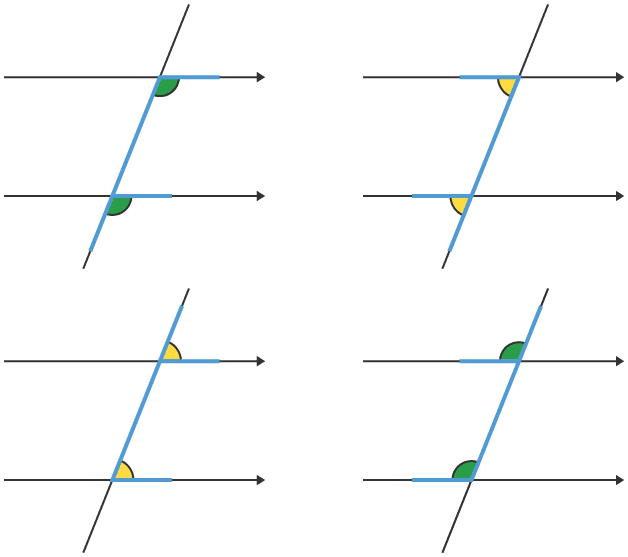
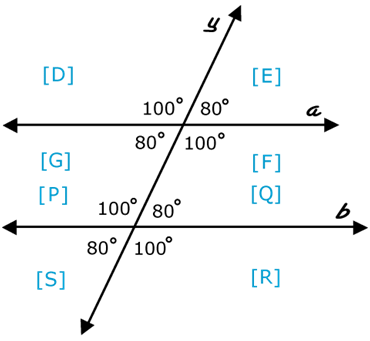
Now let’s mess it up a bit with multiple sets of angles sharing one line, kinda like a road map. Line Y is the transversal line because it joins Lines A and B by crossing them:

We can see that [D] and [E] are supplementary since they share the same vertex, one line (Line Y) and add up to 180^o. What else can we say?

• Corresponding Angles

[E] and [Q] are corresponding angles because they share the same exact position on their parallel lines A and B. Their angles are the same. The same with [F] and [R], [D] and [P], and [G] and [S]. Let’s highlight them:

See how the angle pairs correspond. What else can we say?

• Alternate Interior Angles

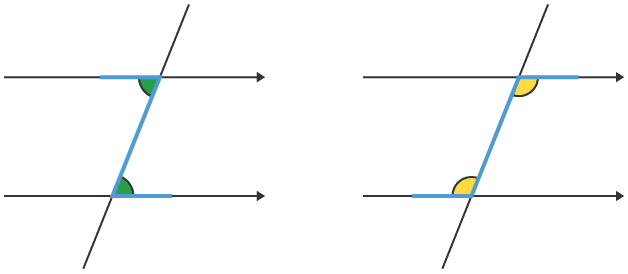
We also have Alternate Interior Angles. Being interior angles, they are on the “inside,” between the parallel lines. These angles share the central transversal line, but have two different vertices. Think of them forming a letter Z and a reverse Z. In the example above, [G] and [Q] are alternate angles. So are [F] and [P]. Since Lines A and B are parallel,we can see that alternate angles have the same degrees.

• Vertically Opposite Angles

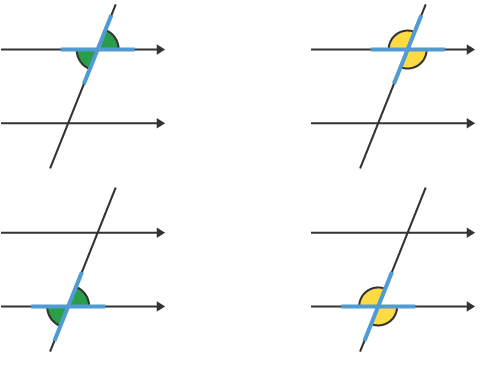
From Z to X!They are angles that share the same vertex and transversal, but no corresponding side. They also have the same degrees. Think of them as the Letter X, with the angles opposite each other. In the above example, [E] and [G] are Vertically Opposite Angles. They each have 80^o. So are [D] and [F]. Each one has 100^o. Check ‘em out below:

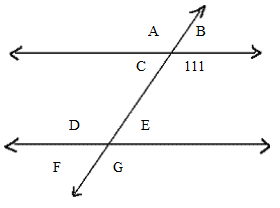
Now that you’re seeing crosses, we’ll have a quick quiz. Find all the angles below:

We only have a single degree measurement, 111^o, but this is no problem, especially if you have an online math tutor to assist.

Solve the SUPPLEMENTARY ANGLE first!

A pair of supplementary angles add up to 180^o, right? We also know that 111^o is OBTUSE, so its adjacent angle, ∠C, must be ACUTE!

∠C + 111^o = 180^o

∠C = 69^o

From there, we can fill out the top set of angles pretty easy.

∠A is a Vertically Opposite Angle from 111^o. We know vertically opposite angles have the same degree measurement. So ∠A is 111^o

The same with ∠C and ∠B.

∠C is 69^o so ∠B is also 69^o.

To check, we can also ADD ∠A + ∠B to see if they add up to 180^o. (They do!)

We can simply copy and paste the top set of angles of the bottom, but we also use our vast knowledge of angle pairings to figure ‘em out. You’re an expert—go right ahead!

∠G is a corresponding angle with 111^o.

That means ∠G =111^o

∠D is an alternate interior angle with 111^o. They form the inverse Z shape!

That means ∠D =111^o

We can either figure out what ∠E and ∠F are since we know their supplementary angles, which add up to 180^o

Or, we can look at them in pairs.

∠E is a corresponding angle with∠B. Since ∠B = 69^o, ∠E is also 69^o.

∠F is a Vertically Opposite Angle from∠E. Since we just figured out what ∠E is, and we know vertically opposite angles have the same value, ∠F is also 69^o.

SO:

∠A = 111^o.

∠B = 69^o.

∠C = 69^o.

∠D = 111^o.

∠E = 69^o.

∠F = 69^o.

∠G = 111^o.

Congrats! You are now the Awesome Angle Master! Have a glimpse of Reference Angles.