Here’s a secret that math tutors keep to themselves: Sometimes, the fanciest math skills are actually the simplest ones! Like the ultra-mysterious Reference Angle! Sounds pretty impressive, no?
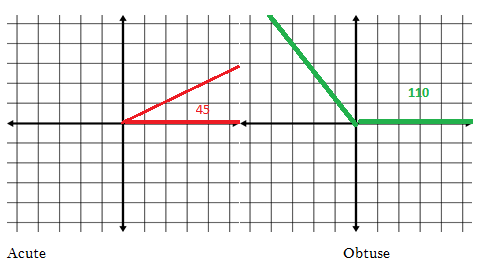
But Reference Angles are actually one of the easiest things to define. Let’s draw a graph and an acute angle (an angle less than 90) and an obtuse angle (an angle that is greater than 90):
The Reference Angles are the measurement of degrees from the shortest distance between the terminal line to the X-axis.
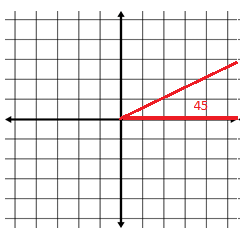
For an acute angle, it is very simple. It is just the degrees.Inn this case, it is 45°.
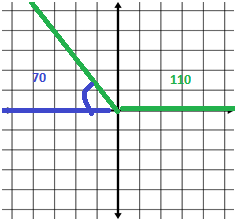
Fort an obtuse angle, it is a little trickier. The terminal line is actually closest to the x-axis on the OPPOSITE side of the angle. In this case, it would be this:
We know the degree measurement is 70° because the angles that make up a straight line through the y-axis is 180°. We just subtract 110° from 180° to get the REFERENCE ANGLE!
If this doesn’t make sense, you can get math homework help from a geometry expert.
***Please note that even though the Reference Angle is on the negative side of the x-axis, it is always positive.
***Also, unless the terminal side of the angle is on the y-axis to form a right angle, the Reference Angle will always be acute!!!
In other words, Reference Angle ≤ 90°
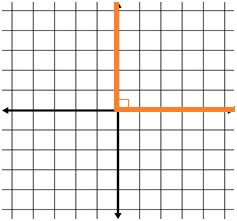
Here is the largest Reference Angle possible:
It is right angle with a measurement of 90°
***We can use Reference Angles to calculate the functions of angles, like sine, cosine, and tangents. It’s basically a cool shortcut: the sin(70) and sin(110) are the same because they have the same Reference Angle!